相似就是一个矩阵在同一空间中不同基之间的变换,而合同是欧式空间中不同基的度量矩阵之间的变换,由于基决定度量矩阵 (度量矩阵是对称正定的,且任意一组标准正交基的度量矩阵是E),而度量矩阵唯一决定内积 ( (α,β)=X^TAY=αβ^T),且正交即内积为0 (即⊥三角形の合同条件を思い出す。 本時の学習内容「2つの三角形が相似になる条件を調べよう」を知る。 課題を考える。 ABCと線分EFがあります。 BC:EF=1:2のとき、 DEFとなる DEFをかきましょう。 対応する辺がすべて1:2となることを確認する。 DEFを合同条件と同じように、最初は辺に注目するよ。 「3組の辺の比がすべて等しい」 ならば、2つの三角形は相似だといえるんだ。 つまり、3組の辺が、 すべて同じ割合で拡大・縮小 されているなら、相似

15考研数学 矩阵的等价 相似 合同的联系及判定 文都考研网
三角形 相似 合同条件
三角形 相似 合同条件- 合同だとわかると 同じ三角形であるのですべてが等しい 相似条件 3辺の比が等しい;相似和合同不能互相推导 雨露学习互助 矩阵相似不合同,举反例谁能帮我举个例子啊,要2个矩阵相似,但是不合同的,实对称矩阵才有相似才合同。 相似和合同不能互相推导 这个不是相当容易的吗,A和B合同的必要条件是AA'和BB'合同 显然相似但不合同




三角形の合同条件はなぜ3つ 証明問題をわかりやすく解説 相似条件との違い 遊ぶ数学
④合同条件(または相似条件)の3つからどれが当てはまるか を探っていきます。 もし、そこで条件が揃っていれば証明は出来ます。 これで解けるのは教科書範囲の問題が多いです。 入試問題では条件が1つ足りないことがよくあります。 そうなった場合は、三角形の合同条件・相似条件の意味について 三角比や正弦定理・余弦定理の理解も深くなる みなさんは、なぜ、合同条件を満たせば合同といえるのか、相似条件を満たせば相似といえるのか?を考えたことがありますか ; p^(1)ap=b;或者:能够找到一个矩阵c,使得a和b均相似于c。 3、进一步地,如果a、b均可相似对角化,则他们相似的充要条件为:a、b具有相同的特征值。 4、再进一步, 因为每个矩阵都相似于唯一一个其标准若尔当型,
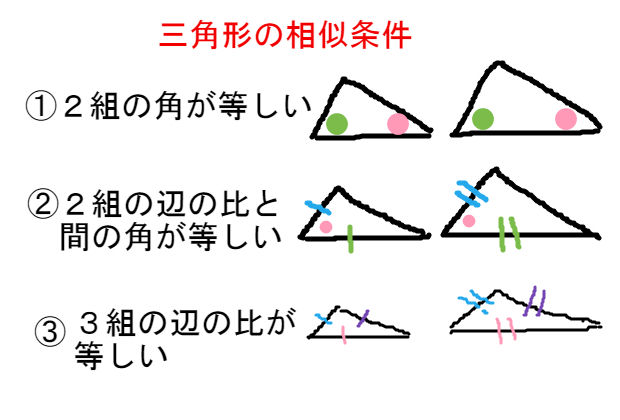
という意味になるように変えることで,三角形の合同条件を三角形の相似条件に変えることができます。 つまり,三角形の相似条件は, 1辺 とその両端の角がそれぞれ等しい→2組の角がそれぞれ等しい となります。 3の条件は,「1組の辺の比とその両端 この場合、2つの三角形は、「2つの角がそれぞれ等しい」っていう相似条件に当てはまるから、相似であるといえるんだ。 種類3 2つの辺が角を挟んでいる条件 つぎは、 2つの辺が角を挟んじゃってる条件 だ。 合同条件と相似条件には2つあるよ。三角形の相似条件 三角形の相似条件 2つの三角形は次の各場合に相似である。 1 3組の辺の比が、すべて等しいとき 2 2組の辺の比とその間の角が、それぞれ等しいとき
動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru矩阵的相似与合同及其等价条件研究 (数学与统计学院 09 级数学与应用数学一班) 指导老师:王晶晶 引言 矩阵的相似与合同及其等价三者在线性代数中是很重要的概念,在线性代数的学 习中,矩阵的相似与合同作为研究工具,得到广泛的应用110,起着非常重要的作用, 能够把要处理的问题証明条件の要素をひとつずつ挙げていく 「〇〇なので、〇〇・・・①」 「〇〇なので、〇〇・・・②」 どの合同条件を満たすのかを書いて結論につなげる 「①②より(相似条件)なので ∽ 」 辺の比が等しいことを示すのは少しややこしく感じるかも



线性代数




保存版 三角形の合同条件と相似条件の6つのまとめ Qikeru 学びを楽しくわかりやすく
1、合同即特征值正负0个数分别相同; 2、相似,特征值相同且都可以对角化或者说特征值相同且都有n个线性无关特征向量; 3、等价,秩相等; 合同和相似是特殊的等价关系。 等价一般是指可以通过初等变换变成另一个,本质上只需要两个矩阵秩相同就可以三角形の相似条件の応用3選 ここまで見ていただいた通り、相似は合同より範囲が広いため、応用範囲も非常に広いです。 よって、最後に「 三角形の相似条件がどのように応用されているか 」代表的なものをご紹介して終わりにします。 Ppt 相似条件と証明 Powerpoint Presentation Free Download Id 三角形の相似条件と有名な例題3問 具体例で学ぶ数学 相似 三角形の相似条件 記号や証明問題も Studyplus スタディプラス 三角形の相似の証明の解き方 現役塾講師のわかりやすい中学数学の解き方 三角形の
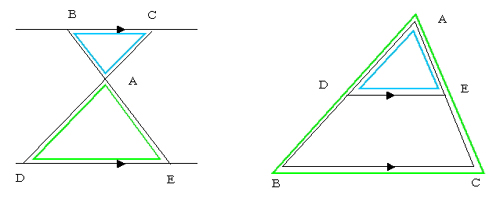



相似 直角三角形
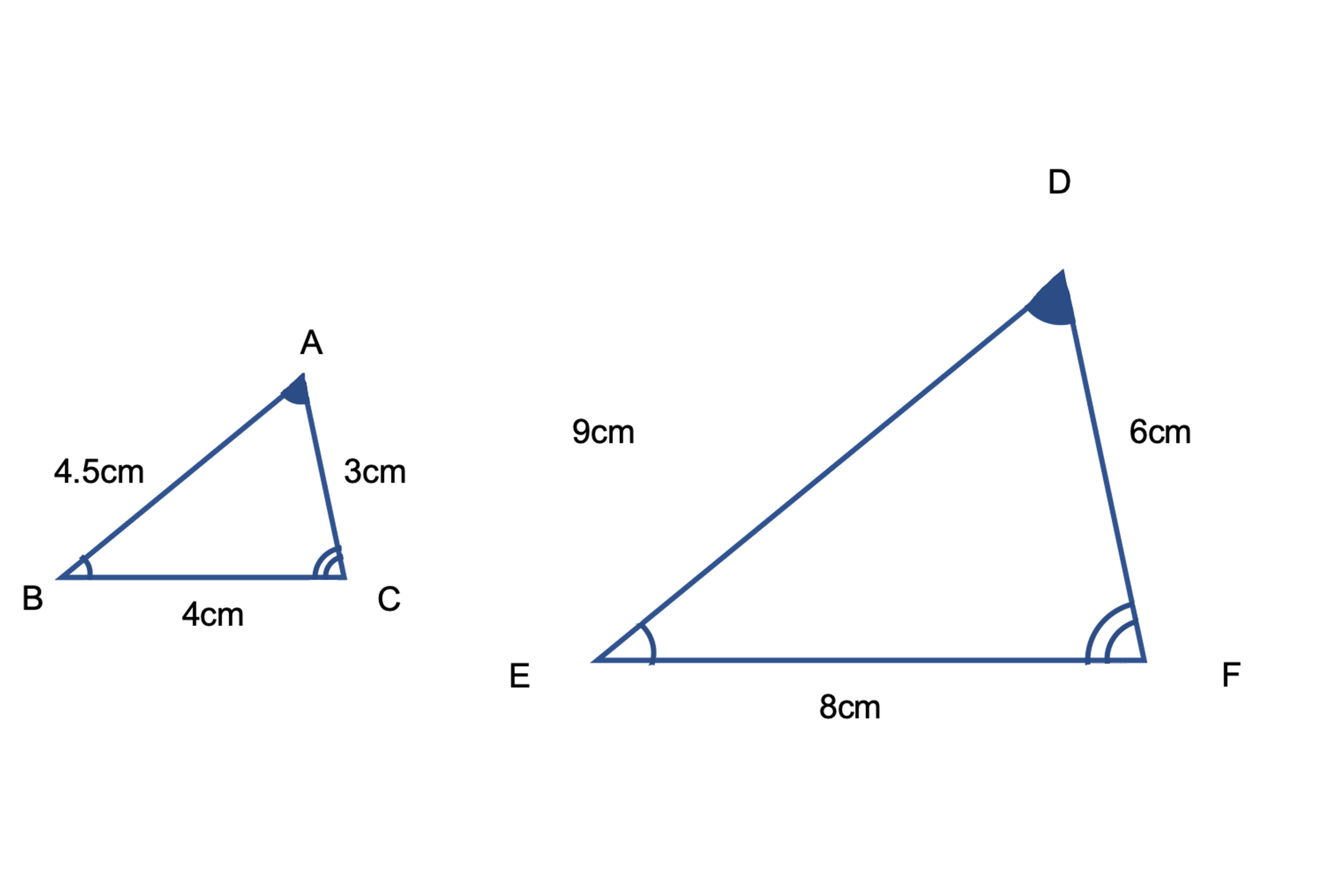



記号にすると と 三角形の 合同 と 相似 の違いをまとめよう 受験に関する豆知識 学習塾ランキング検索総合サイト 塾プラス
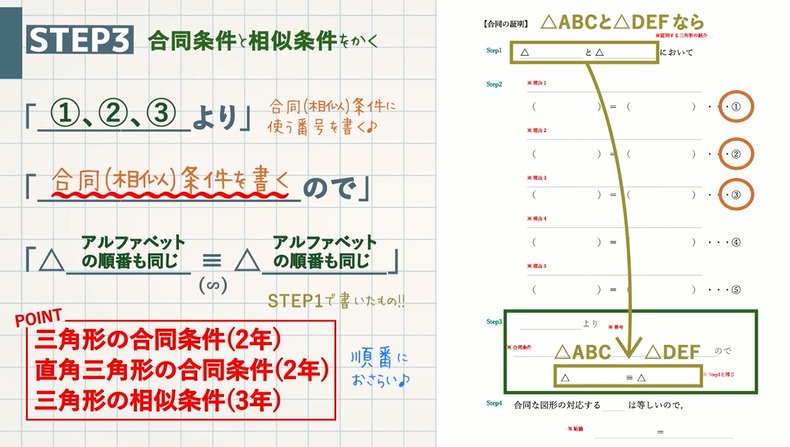
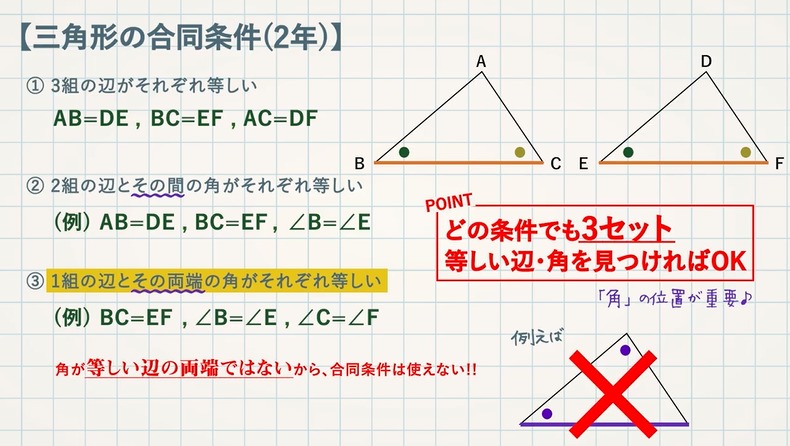
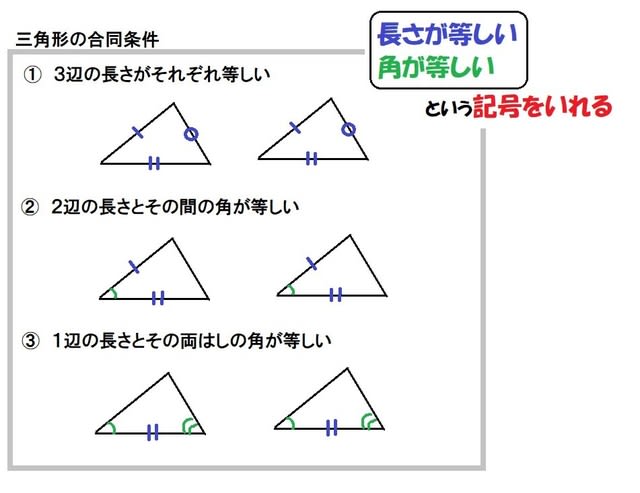
STEP3:合同条件と相似条件をかく 6:27 等しい辺や角を理由とともに説明したら、 合同条件・相似条件をかきます。 「 ①,②,③ より」 →合同 (相似)条件に使う番号を書きます。 「 合同 (相似)条件を書く ので」 「 〇〇〇≡ (∽) 〇〇〇 」 →STEP 1 の 2 条件③ 1組の辺とその両端の角がそれぞれ等しい 1組の辺の長さと、その両端の角がそれぞれ等しいとき「それらの三角形は合同である」ということができます。 上図の場合、 B C = E F 、 ∠ B = ∠ E 、 ∠ C = ∠ F で1組の辺の長さとその両端の角がそれぞれ等しいことから、合同となります。相似条件 まとめ 相似な図形を見つけるためには 辺の長さや角の大きさを比較して 3組の辺の比がすべて等しい;




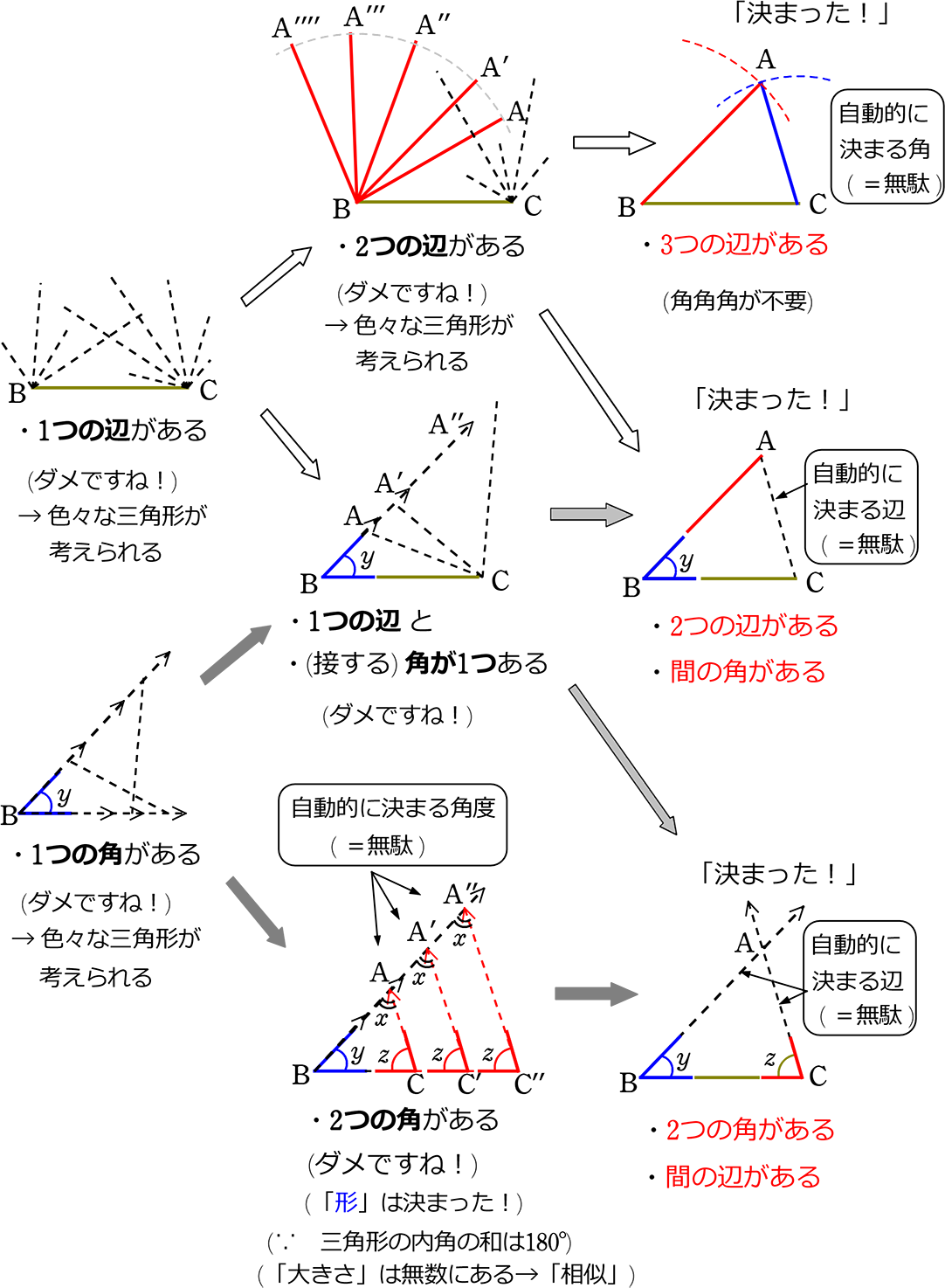
三角形の合同条件で 3組の角はそれぞれ等しい と言うのがないのは何故でしょうか Clear




三角形の 合同条件 相似条件 の意味について 三角比や正弦定理 余弦定理の理解も深くなる ここからはじめる高校数学
単元 三角形, 「三角形の相似条件・合同条件 平行四辺形・直角三角形・二等辺三角形 についてです。」, 学年 中学全学年, キーワード 数学,中1,中2,中3,中学,中学生,中学校,相似,合同,相似条件,合同条件,平行四辺形,直角三角形,二等辺三角形,math




第16讲相似矩阵与方阵的对角化主要内容 1 相似矩阵2 方阵的对角化 Ppt Download




条款和条件的图标相似素材图片 摄图新视界



每日一题讲解 Math业精于勤 微信公众号文章阅读 Wemp



証明 合同 相似 が苦手な人へ 教遊者




特征值相同的两个矩阵是否相似 寻找自由的咸鱼的博客 Csdn博客 特征值相同的矩阵相似吗
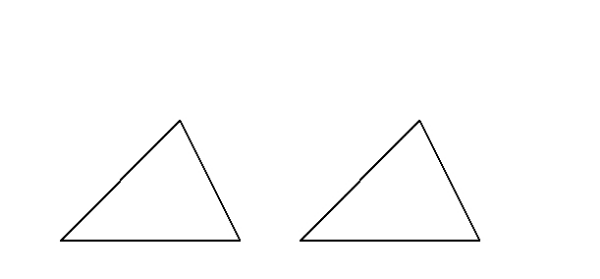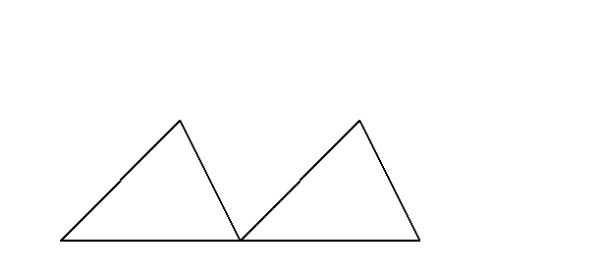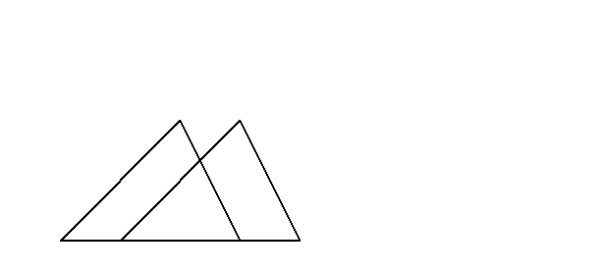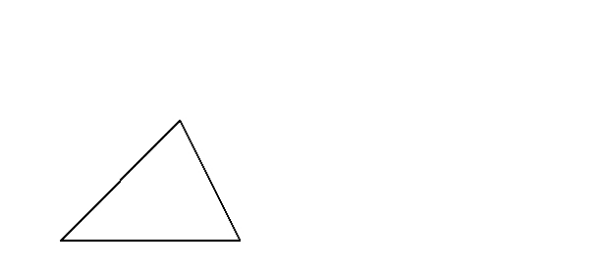



三角形の 合同条件 相似条件 の意味について 三角比や正弦定理 余弦定理の理解も深くなる ここからはじめる高校数学



Www Pref Chiba Lg Jp Kyouiku Shidou Gakuryoku Zissenmoderu Documents C 047 Pdf
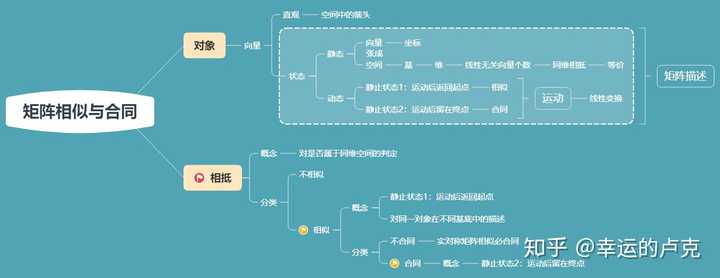



如何形象地理解矩阵的相似与合同 知乎



中学数学 図形の合同 図形の性質




1 1 2 1i 322 23 2a2 Cme5 Descubre Como Resolverlo En Qanda




相似条件 合同条件 中学生 数学のノート Clear




上数学合同条件 ニスヌーピー壁紙




17考研数学 矩阵合同与相似的典型题型分析 文都考研网



三角形の相似条件と証明問題の解き方 数学fun



股权激励合同中的巨额离职违约金条款是否违法 至本精彩问答 至本咨询 股权设计中心



平面図形の基礎



Www Nisimino Com Bunkyo Pdf Ronbun H26 13 Pdf




合同条款和条件图标 商业服务理念 矢量插图相似素材图片 摄图新视界



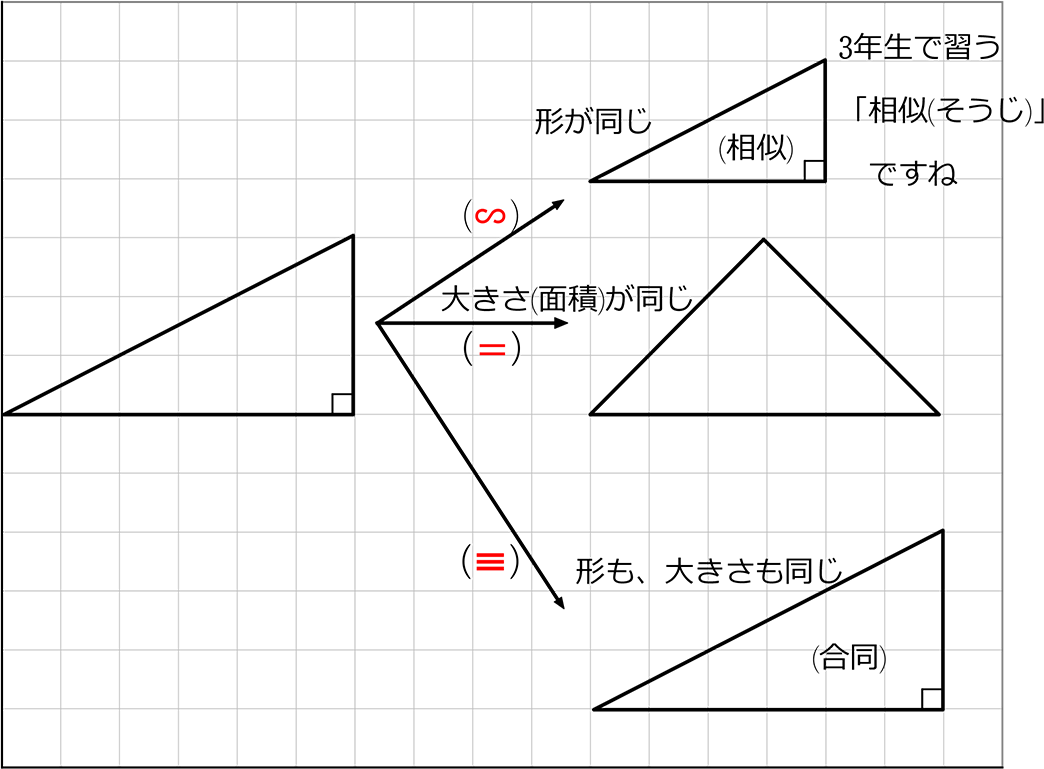
合同と相似とは 演習問題にチャレンジ 個別指導のオンライン家庭教師wam



矩阵的合同相似等价为什么这么定义呢 哔哩哔哩 Bilibili



Fidic 17版银皮书与黄皮书风险分担比较分析 建纬观点 上海市建纬 郑州 律师事务所



相似条件や合同条件は定義ですか 相似 合同条件は 定義ではなく Yahoo 知恵袋



合同 相似条件の書き方 中学から数学だいすき



三角形の合同条件と相似条件を教えてください 三角形の合同条件と相似 Yahoo 知恵袋




Mathnaviレクチャー 学びをつなげよう 3年5章 図形と相似 三角形の合同条件 Youtube




17考研數學中如何判定矩陣合同關係 壹讀



証明 合同 相似 が苦手な人へ 教遊者




第四章第一节合同履行的意义一 是合同效力的必然要求 是实现合同利益的根本措施二 是合同关系消灭的主要原因 是加速经济流转的重要前提




普通矩阵相似不一定合同 步行街主干道 虎扑社区
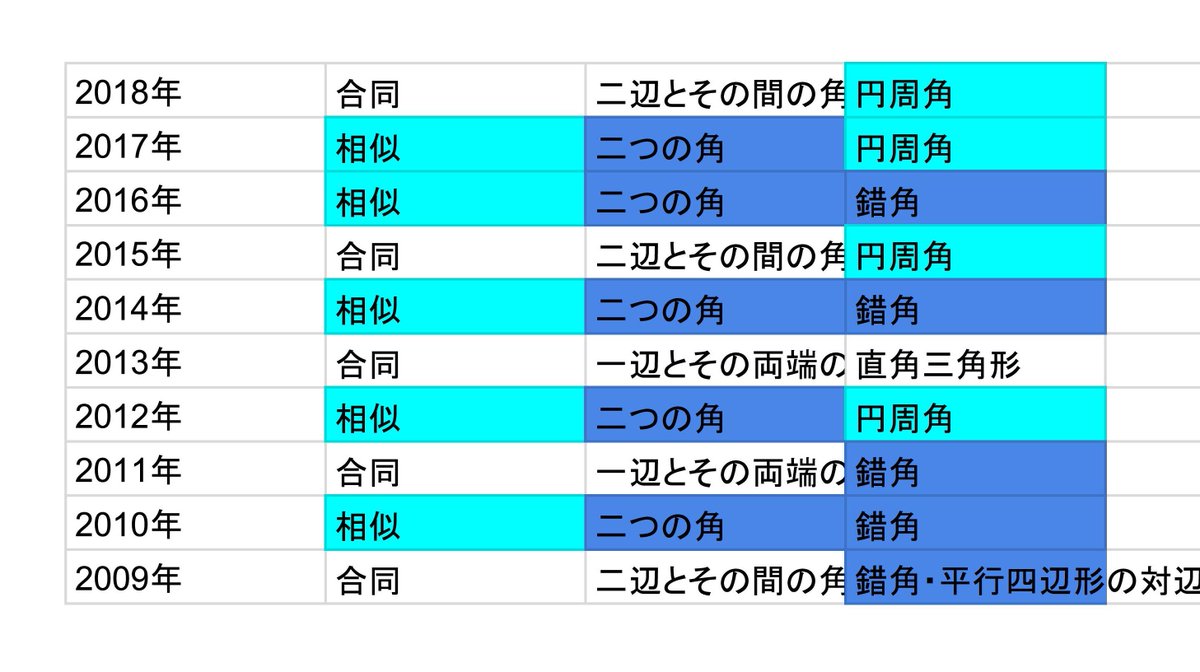



相似条件




矩阵等价合同相似符号矩阵等价合同相似的符号分别是什么啊是这样的吗 我们的教材 代表相似 合同是图中的等价符号 那种对




讲稿 矩阵合同相似下载 Word模板 爱问共享资料



合同 相似条件の書き方 中学から数学だいすき
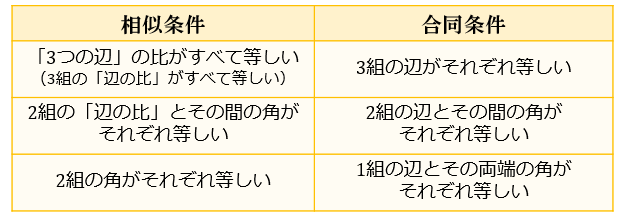



三角形の合同条件 相似条件と合同条件の違いとは アタリマエ




考研数学 令人头大的相似 合同 等价 复习经验 考研帮 Kaoyan Com




都立高校入試数学の法則 2 図形の証明問題 相似と合同 どちらが出る 都立に入る



工程行业国际知名合同范本比较分析报告 译问




保存版 三角形の合同条件と相似条件の6つのまとめ Qikeru 学びを楽しくわかりやすく




三角形の合同条件はなぜ3つ 証明問題をわかりやすく解説 相似条件との違い 遊ぶ数学




合同条件の選び方 家庭教師学参 群馬県のブログ




矩阵相关定义性质全总结 I Canjnu的博客 程序员宅基地 矩阵性质总结 程序员宅基地




矩阵等价 相似 合同的判断 参考网



Http Kylaboratory Com Wp Wp Content Uploads 19 05 7e545a0eb76b786cecac0e7699 Pdf




中学生 数学苦手no 2 証明問題 合同 相似 の解き方 学習内容解説ブログ




矩阵的合同相似等价为什么这么定义呢 哔哩哔哩 Bilibili



工程行业国际知名合同范本比较分析报告 译问



相似とは 三角形の相似条件 記号 相似比 面積比 証明問題 受験辞典




矩阵等价 相似 合同之间的区别和联系 百度知道
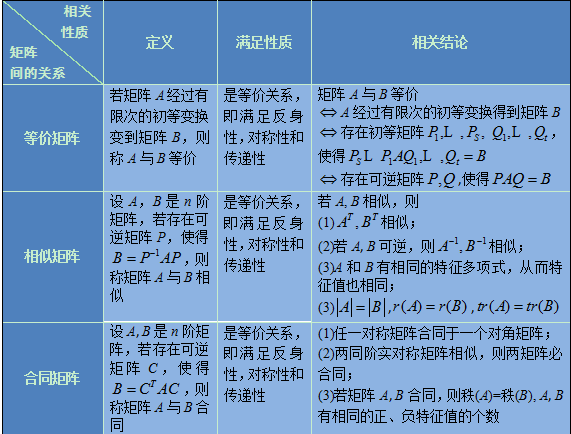



等价矩阵 相似矩阵 合同矩阵 Mjiansun的专栏 Csdn博客




Ab相似的充要条件 A与b合同的充要条件为 矩阵ab相似的充要条件




保存版 三角形の合同条件と相似条件の6つのまとめ Qikeru 学びを楽しくわかりやすく




三角形の合同条件 Youtube




国际工程合同谈判策略与技巧 1 下载 Word模板 爱问共享资料




Pdf Fidic红皮书 中文 1 Miao Zhang Academia Edu
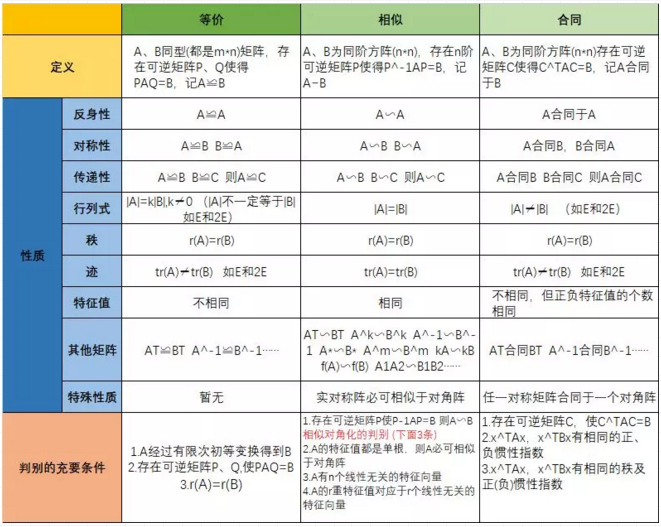



考研数学 令人头大的相似 合同 等价 复习经验 考研帮 Kaoyan Com



三角形の相似 合同条件 中学数学 理科 寺子屋塾の復習サイト




保存版 三角形の合同条件と相似条件の6つのまとめ Qikeru 学びを楽しくわかりやすく




2 1 Y3 bbcc A A B A Descubre Como Resolverlo En Qanda




三角形の相似 合同条件 中学数学 理科 寺子屋塾の復習サイト



上数学合同条件 ニスヌーピー壁紙



中学数学 図形の合同 図形の性質




15考研数学 矩阵的等价 相似 合同的联系及判定 文都考研网




三角形の相似条件と証明問題の解き方 数学fun



証明 合同 相似 が苦手な人へ 教遊者



Www Tsumugi Ne Jp Pdf Step3 3 6 2 Pdf
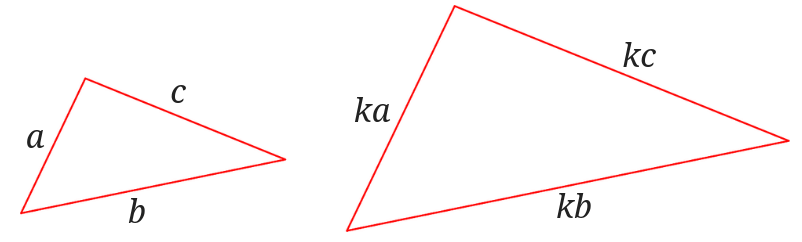



相似な図形と三角形の相似条件 まぜこぜ情報局
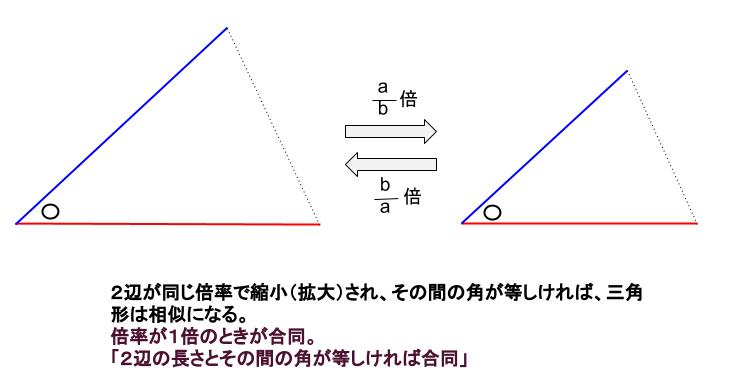



中学数学 三角形の相似条件 中学数学の無料オンライン学習サイトchu Su




工程建设招标设标合同合同条件word模板下载 招标 熊猫办公




保存版 三角形の合同条件と相似条件の6つのまとめ Qikeru 学びを楽しくわかりやすく
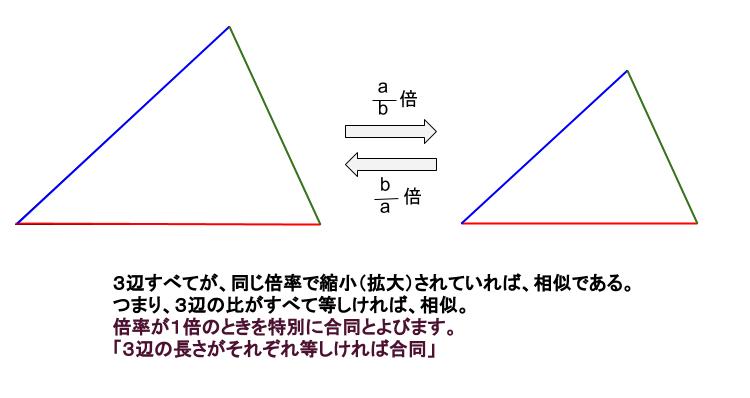



中学数学 三角形の相似条件 中学数学の無料オンライン学習サイトchu Su



70以上直角三角形相似条件 ニーアオートマタ壁紙



工程行业国际知名合同范本比较分析报告 译问




三角形の合同条件 相似条件と合同条件の違いとは アタリマエ




合同と相似とは 演習問題にチャレンジ 個別指導のオンライン家庭教師wam
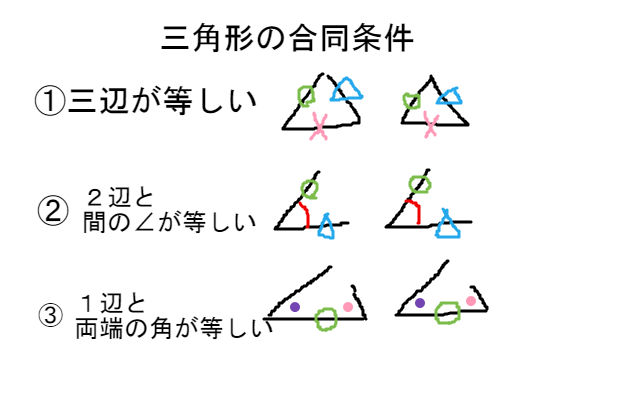



三角形の相似 合同条件 中学数学 理科 寺子屋塾の復習サイト




上数学合同条件 ニスヌーピー壁紙
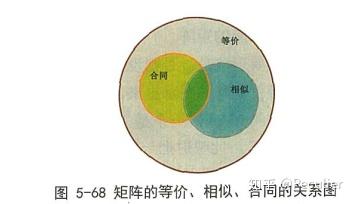



矩阵的等价 相似及合同 知乎
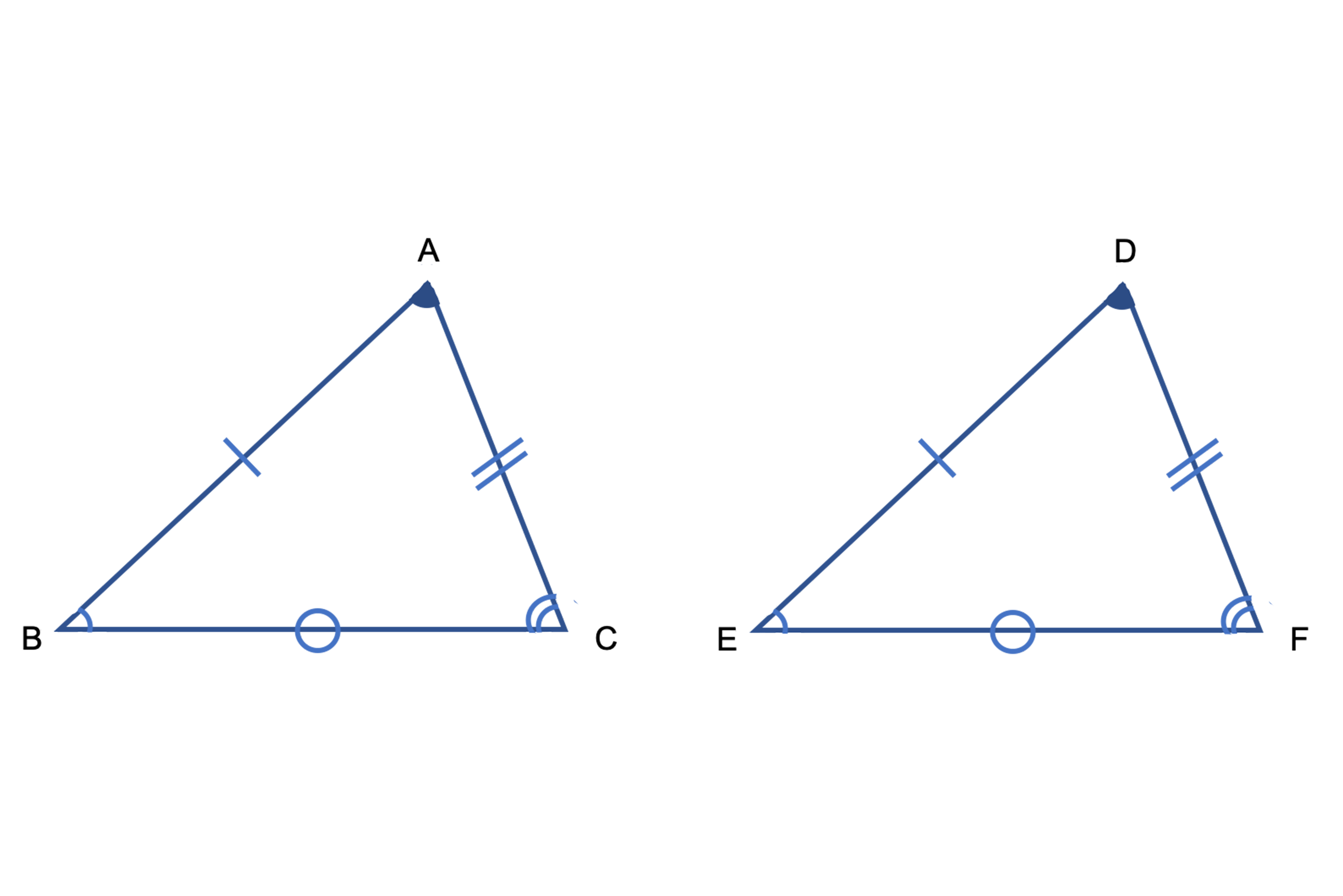



記号にすると と 三角形の 合同 と 相似 の違いをまとめよう 受験に関する豆知識 学習塾ランキング検索総合サイト 塾プラス




Nkaw32znbbhnkm




工程建设招标设标合同合同条件 第2部分 Word模板下载 招标合同 熊猫办公




仕事の問題です やり方を教えて下さい Clear




年度用 中学校数学教科書内容解説資料 未来へひろがる数学
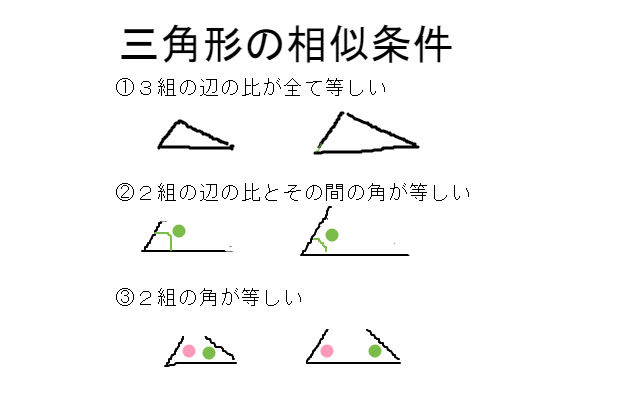



ぜいたく直角三角形相似条件 壁紙配布




三角形の相似条件と証明問題の解き方 数学fun



合同矩阵 快懂百科
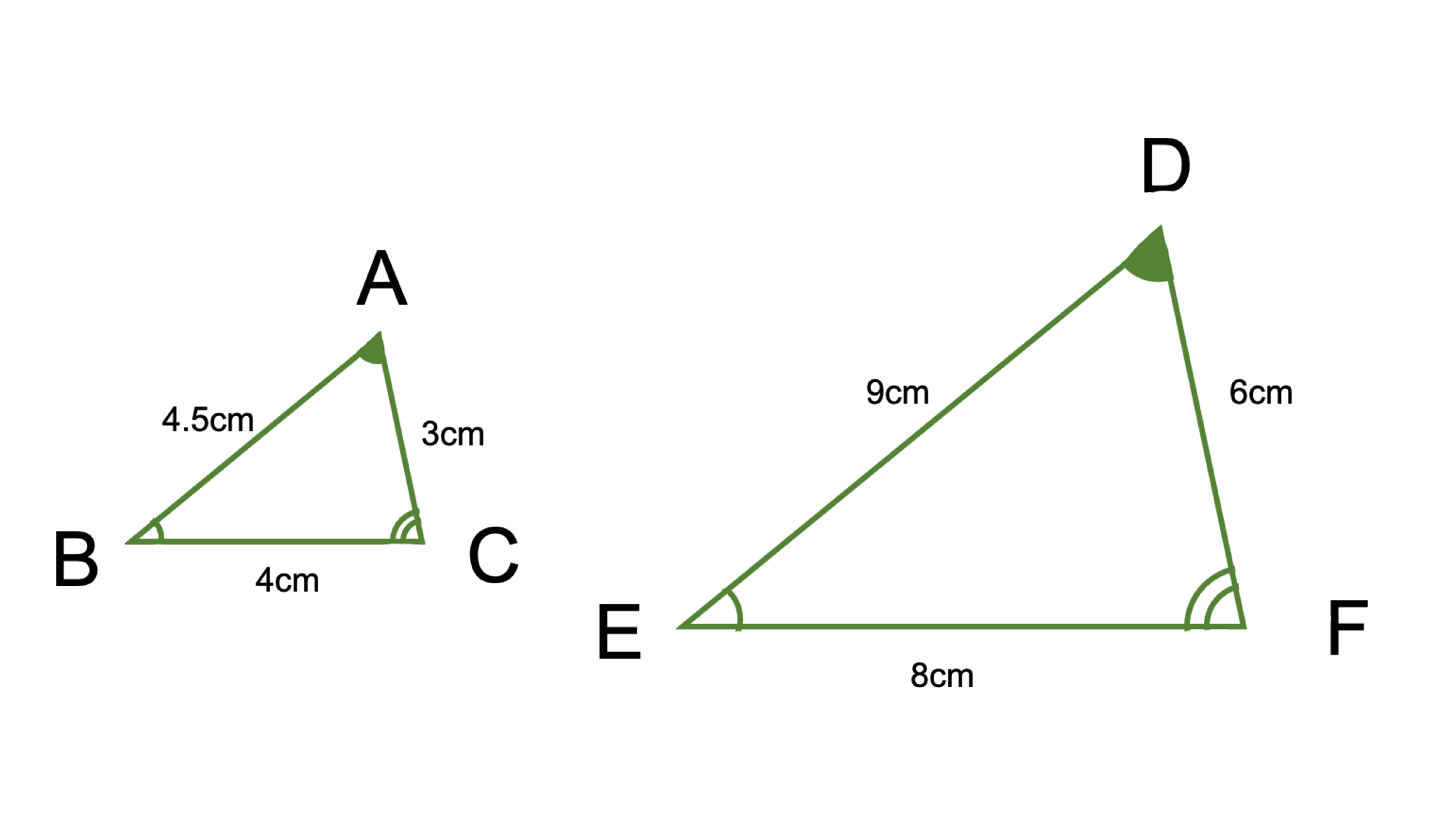



三角形の 合同条件 とは 直角三角形の2つも覚えて証明問題を攻略しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード
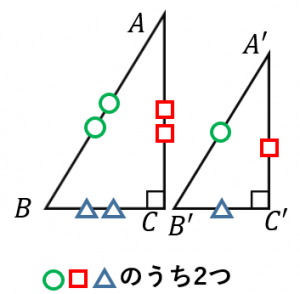



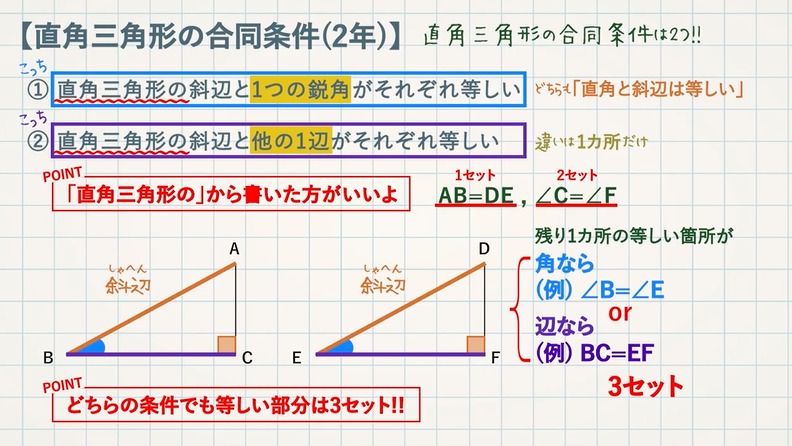
直角三角形の相似条件 具体例で学ぶ数学




三角形の合同条件はなぜ3つ 証明問題をわかりやすく解説 相似条件との違い 遊ぶ数学




三角形の合同条件はなぜ3つ 証明問題をわかりやすく解説 相似条件との違い 遊ぶ数学




三角形の合同条件はなぜ3つ 証明問題をわかりやすく解説 相似条件との違い 遊ぶ数学




三角形の合同条件 相似条件と合同条件の違いとは アタリマエ
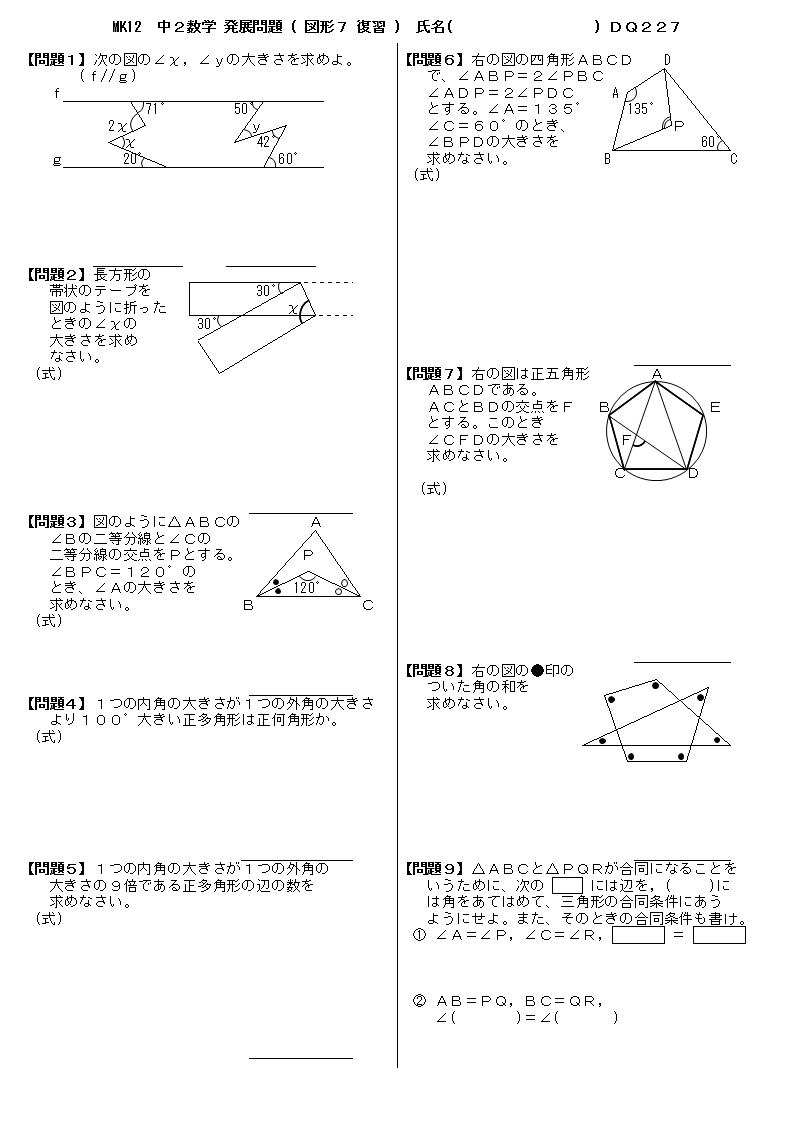



無料 中2数学 応用 発展問題 問題プリント 327 図形の相似2 相似条件と証明
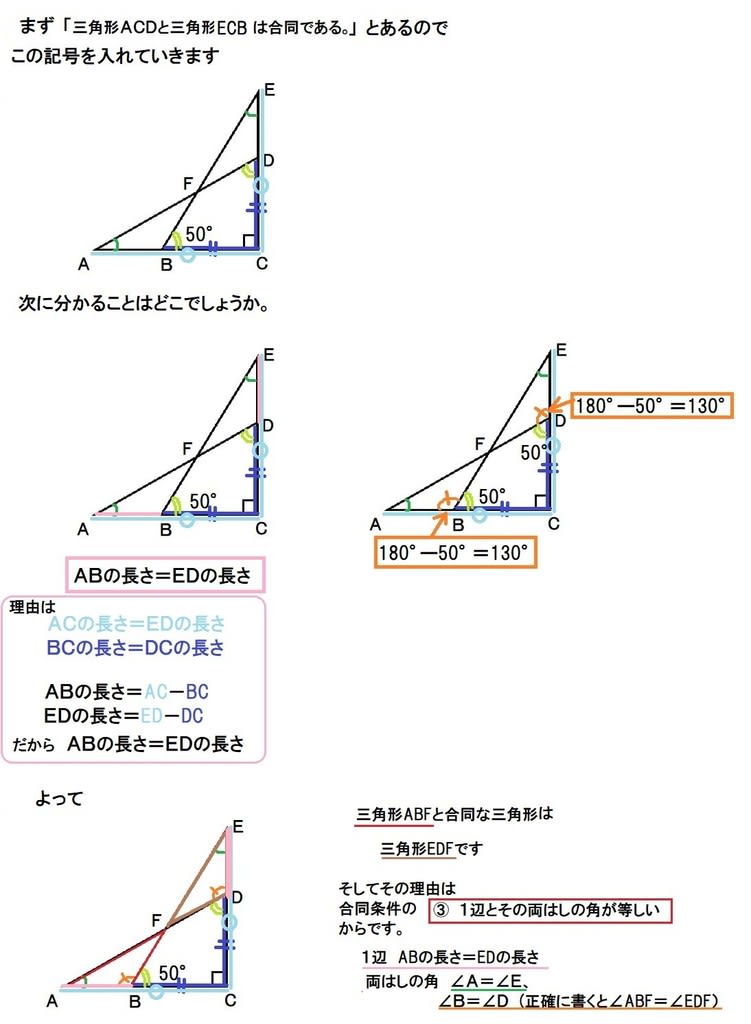



合同な図形 小5 合同条件は超重要 算数の教え方教えますmother S Math Happy Study Support
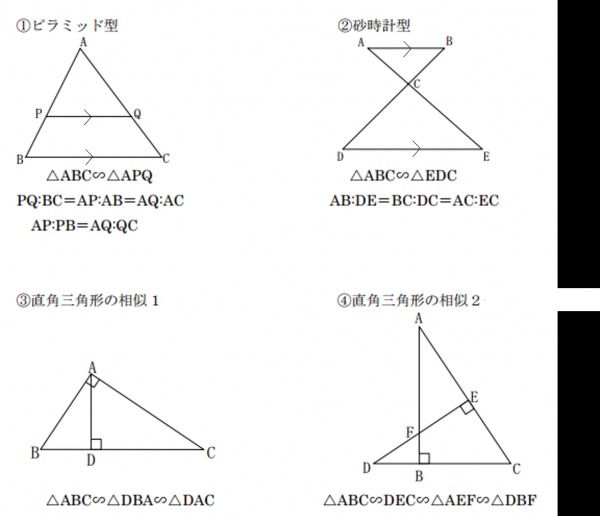



三角形の相似 合同条件 優技録



0 件のコメント:
コメントを投稿